高三数学抛物线练习题

时间：2023-05-02 16:09:22 数学试题我要投稿

相关推荐

高三数学抛物线练习题

　　1.已知抛物线y=ax2的准线方程为y=1，则a的值为

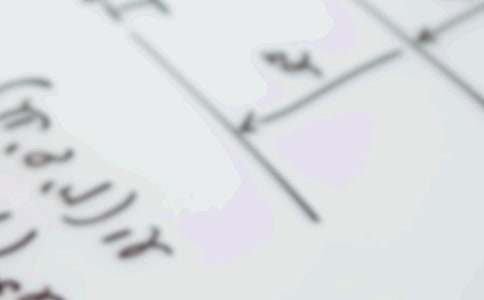
高三数学抛物线练习题

　　()

　　A.4 B.-14

　　C.-4 D.14

　　答案：B

　　2.(2013四川)抛物线y2=8x的焦点到直线x-3y=0的距离是

　　()

　　A.23 B.2

　　C.3 D.1

　　解析：由抛物线方程知2p=8p=4，故焦点F(2,0)，由点到直线的距离公式知，F到直线x-3y=0的距离d=|2-30|1+3=1.故选D.

　　答案：D

　　3.设抛物线y2=8x的焦点为F，准线为l，P为抛物线上一点，PAl，A为垂足.如果直线AF的斜率为-3，那么|PF|等于

　　()

　　A.43 B.8

　　C.83 D.16

　　解析：设Py28，y，则A(-2，y)，

　　由kAF=-3，即y-0-2-2=-3

　　得y=43，

　　|PF|=|PA|=y28+2=8.

　　答案：B

　　4.(2013山东)抛物线C1：y=12px2(p0)的焦点与双曲线C2：x23-y2=1的右焦点的连线交C1于第一象限的点M.若C1在点M处的切线平行于C2的一条渐近线，则p=

　　()

　　A.316 B.38

　　C.233 D.433

　　解析：设抛物线C1的焦点为F，则F0，p2.

　　设双曲线C2的右焦点为F1，则F1(2,0).

　　直线FF1的方程为y=-p4x+p2，设Mx0，x202p，因为M在直线FF1上，x202p=-p4x0+p2.①

　　∵y=12px2，y=1px，C1在M点处的切线斜率为1px0，又x23-y2=1的渐近线方程为y=33x，故由题意得1px0=33，②

　　将①、②联立得p=433，故选D.

　　答案：D

　　5.若抛物线的焦点在直线x-2y-4=0上，则抛物线的标准方程是________.

　　解析：x-2y-4=0与两轴的交点为(0，-2)，(4,0)

　　方程y2=16x，x2=-8y.

　　答案：y2=16x或x2=-8y

　　6.已知抛物线y2=4x上一点M与该抛物线的焦点F的距离|MF|=4，则点M的横坐标x=________.

　　解析：抛物线y2=4x的焦点为F(1,0)，准线为x=-1.根据抛物线的定义，点M到准线的距离为4，则M的横坐标为3.

　　答案：3

　　7.(2013安徽)已知直线y=a交抛物线y=x2于A，B两点.若该抛物线上存在点C，使得ACB为直角，则a的取值范围为________.

　　解析：法一：如图，以(0，a)为圆心，a为半径作圆，当圆与抛物线有三个或四个交点时，C存在.

　　联立y=x2，x2+(y-a)2=a有(y-a)(y-a+1)=0.

　　即y=a或y=a-1.故a-10，即a1.

　　法二：当C与原点重合时，ACB最小.故若存在C使得ACB为直角，则2，即OAOB0，故a2-a0，又a0，所以a1.

　　答案：[1，+)

　　8.抛物线的顶点在原点，以x轴为对称轴，经过焦点且倾斜角为135的直线，被抛物线所截得的弦长为8，试求抛物线方程.

　　解：如图，依题意设抛物线方程为y2=2px(p0)，

　　则直线方程为y=-x+12p.

　　设直线交抛物线于A(x1，y1)、B(x2，y2)，则由抛物线定义得|AB|=|AF|+|FB|=|AC|+|BD|=x1+p2+x2+p2，

　　即x1+p2+x2+p2=8.①

　　又A(x1，y1)、B(x2，y2)是抛物线和直线的交点，

　　由y=-x+12p，y2=2px，消去y得x2-3px+p24=0.

　　x1+x2=3p.

　　将其代入①得p=2，所求抛物线方程为y2=4x.

　　当抛物线方程设为y2=-2px时，同理可求得抛物线方程为y2=-4x.

　　综上，抛物线的方程为y2=4x.

　　9.(2014河南洛阳期中考试)已知抛物线C：x2=2py(p0)，O为坐标原点，F为抛物线的焦点，直线y=x与抛物线C相交于不同的两点O、N，且|ON|=42.

　　(1)求抛物线C的方程;

　　(2)若直线l过点F交抛物线于不同的两点A，B，交x轴于点M，且MA=aAF，MB=bBF，对任意的直线l，a+b是否为定值?若是，求出a+b的值;否则，说明理由.

　　解：(1)联立方程y=xx2=2py得x2-2px=0，故O(0,0)，N(2p,2p)，|ON|=4p2+4p2=22p，

　　由22p=42得p=2，抛物线C的方程为x2=4y.

　　(2)显然直线l的斜率一定存在且不等于零，设其方程为y=kx+1，则直线l与x轴交点为M-1k，0

　　记点A(x1，y1)，B(x2，y2)，

　　由y=kx+1x2=4y得x2-4kx-4=0，

　　=(4k)2-(-16)=16(k2+1)0，

　　x1+x2=4k，x1x2=-4.

　　由MA=aAF，得x1+1k，y1=a(-x1,1-y1)，

　　a=y11-y1=-kx1+1kx1，同理可得b=-kx2+1kx2，

　　a+b=-kx1+1kx1+kx2+1kx2=-2+x2+x1kx1x2

　　=-1，

　　对任意的直线l，a+b为定值-1.

【高三数学抛物线练习题】相关文章：

抛物线作文10-01